0 BAB PELUANG
Assalamualaikum Wr.Wb
Bab peluang anda katakan apakah sulit untuk dipelajari???
Jika memang ia anda mengatakan begitu, mari kita belajar bersama dan berbagi ilmu bersama disini.
Untuk dapat memahami Peluang, Kalian harus memahami Kaidah Pecahan terlebih dahulu.
Apa itu kaidah pecahan???
Kaidah pecahan adalah Kaidah bagaimana kita mencoba menemukan berapa banyaknya hasil yang mungkin terjadi (muncul) pada berbagai percobaan. Untuk menemukan banyaknya hasil yang mungkin muncul pada suatu percobaan biasanya di SMA menggunakan pendekatan-pendekatan sebagai berikut :
1. Kaidah perkalian.
2. Permutasi
3. Kombinasi
Dari ketiga pendekatan-pendekatan tersebut mari kita bahas, dan mempelajarinya satu demi satu.
mulai dari yang pertama yaitu :
1. Kaidah perkalian.
Kaidah perkalian mengatakan bahwa :
Jika tempat pertama dapat diisi dengan n1 cara yang berbeda, tempat kedua dengan n2 cara,...,
tempat ke-k dengan nk cara, maka banyaknya cara untuk mengisi k tempat yang tersedia adalah
n1 x n2 x . . . x nk.
Apakah kalian sudah tahu penjelasan di atas?. Jiak belum mari kita mengerjaka soal Sipenmaru
1985 di bawah ini agar menjadi lebih paham.
Soal Kaidah perkalian.
Bila kita perhatikan nomor rumah yang terdiri atas dua angka , tanpa
angka nol, maka banyak rumah yang dimaksud dengan nomor ganjil adalah . . .
Pembahasan Kaidah perkalian.
Untuk dapat menjawab soal diatas maka kita perhatikan soalnya terlebih dahulu dengan seksama
dan teliti.
Nomor rumah yang dimaksud terdiri atas dua angka. ini berarti ada dua tempat yang harus diisi,
yaitu PULUHAN dan SATUAN. Karena nomor rumah harus ganjil maka tempat satuan hanya
dapat diisi oleh bilangan-bilangan ganjil saja, yaitu : 1,3,5,7,9. dengan demikian ada 5 cara untuk
mengisi tempat satuan, sehingga n1 = 5. Sedangkan tempat puluhan dapat diisi oleh angka
1,2,3,4,5,6,7,8,9. Sehingga didapat n2 = 9. Dengan demikian banyaknya nomor rumah dengan
nomor ganjil adalah n1 x n2 = 5x9 = 45.
Mudah bukan?.
Selanjutnya kita melangkah ke pendekatan yang kedua yaitu permutasi.
2. Pertmutasi
Apakah kalian sudah tahu apa itu permutasi?
ya, permutasi adalah suatu susunan unsur-unsur berbeda dalam urutan tertentu. pada permutasi
urutan diperhatikan, sehingga AB tidak samadenga BA.
Permutasi sendiri ada tiga macam.
adalah banyak permutasi r unsur dari n unsur, yang dinotasikan dengan P(n,r) detentukan oleh rumus:
Permutasi yang kedua yaitu dengan beberapa unsur yang sama.
adalah banyaknya permutasi dari n unsur yang memiliki r1 unsur pertama yang sama, r2 unsur kedua yang sama, . . . , dan rk unsur ke-k yang sama. Perhatika rumus dibawah ini!!!
Permutasi yang ketiga yaitu permutasi siklis.
adalah banyaknya permutasi siklis ( melingkar ) dari n unsur. Perhatikan rumus dibawah ini.
Rumus . (n-1)!
Setelah anda membaca tentang permutasi di atas apakah anda sudah memahaminya?
Jika sudah, coba kalian kerjakan soal dibawah ini, apakah menggunakan permutasi yang pertama,yang kedua, atau yang ketiga.
Perhatika soalnya baik-baik yah?
Soal Permutasi.
EBTANAS 1994.
Untuk menjabat pengelola suatu perusahaan memerlukan 3 staf pengurus yaitu ketua, sekretaris, dan bendahara. Tersedia 7 calon. banyaknya macam susunan staf pengurus yang mungkin adalah . . .
Apakah kalian bisa mengerjakan?, Pasti bisa donk yan?
mari kita cocokan pekerjaan kalian.
Pembahasan Permutasi.
Jika susunan staf pengurus adalah ABC, maka A sebagai ketua, B sebagai SEkretaris dan C sebagai bendahara. terapi jika susunan staf pengurus adalah , CBA maka C sebagai ketua, B sebagai Sekretaris dan A sebagai bendahara. Jadi jelas bahwa ABC tidak samadengan CBA. Ini berarti soal diatas memperhatikan urutan. Dengan demikian kita selesaikan dengan cara permutasi. pada soal diketahui bahwa akan dipilih 3 orang untuk menjadi staf Pengurusdari 7 orangcalon yang tersedia.
Hal ini merupakan permutasi 3 unsur dari 7 unsur. dengan demikian banyaknya susunan pengurus yang mungkin adalah .
3. Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutan.
Rumus Kombinasi Adalah
Contoh soal Kombinasi.
1. ada lima orang dalam satu ruangan yang belum saling mengenal. apabilamereka ingin saling berkenalan dengan berjabat tangn sekali dengan setiap orang. maka banyaknya jabatan tangn yang terjafi adalah . . .
a. 5 kali
b. 10 kali
c. 15 kali
d. 20 kali
e. 25 kali
Semoga bermanfaat dan sukses buat kita semua dan lulus 100%. Amin.
trimakasih Wassalamualaikum Wr.Wb.
Sumber: http://sharematika.blogspot.no/
Bab peluang anda katakan apakah sulit untuk dipelajari???
Jika memang ia anda mengatakan begitu, mari kita belajar bersama dan berbagi ilmu bersama disini.
Untuk dapat memahami Peluang, Kalian harus memahami Kaidah Pecahan terlebih dahulu.
Apa itu kaidah pecahan???
Kaidah pecahan adalah Kaidah bagaimana kita mencoba menemukan berapa banyaknya hasil yang mungkin terjadi (muncul) pada berbagai percobaan. Untuk menemukan banyaknya hasil yang mungkin muncul pada suatu percobaan biasanya di SMA menggunakan pendekatan-pendekatan sebagai berikut :
1. Kaidah perkalian.
2. Permutasi
3. Kombinasi
Dari ketiga pendekatan-pendekatan tersebut mari kita bahas, dan mempelajarinya satu demi satu.
mulai dari yang pertama yaitu :
1. Kaidah perkalian.
Kaidah perkalian mengatakan bahwa :
Jika tempat pertama dapat diisi dengan n1 cara yang berbeda, tempat kedua dengan n2 cara,...,
tempat ke-k dengan nk cara, maka banyaknya cara untuk mengisi k tempat yang tersedia adalah
n1 x n2 x . . . x nk.
Apakah kalian sudah tahu penjelasan di atas?. Jiak belum mari kita mengerjaka soal Sipenmaru
1985 di bawah ini agar menjadi lebih paham.
Soal Kaidah perkalian.
Bila kita perhatikan nomor rumah yang terdiri atas dua angka , tanpa
angka nol, maka banyak rumah yang dimaksud dengan nomor ganjil adalah . . .
Pembahasan Kaidah perkalian.
Untuk dapat menjawab soal diatas maka kita perhatikan soalnya terlebih dahulu dengan seksama
dan teliti.
Nomor rumah yang dimaksud terdiri atas dua angka. ini berarti ada dua tempat yang harus diisi,
yaitu PULUHAN dan SATUAN. Karena nomor rumah harus ganjil maka tempat satuan hanya
dapat diisi oleh bilangan-bilangan ganjil saja, yaitu : 1,3,5,7,9. dengan demikian ada 5 cara untuk
mengisi tempat satuan, sehingga n1 = 5. Sedangkan tempat puluhan dapat diisi oleh angka
1,2,3,4,5,6,7,8,9. Sehingga didapat n2 = 9. Dengan demikian banyaknya nomor rumah dengan
nomor ganjil adalah n1 x n2 = 5x9 = 45.
Mudah bukan?.
Selanjutnya kita melangkah ke pendekatan yang kedua yaitu permutasi.
2. Pertmutasi
Apakah kalian sudah tahu apa itu permutasi?
ya, permutasi adalah suatu susunan unsur-unsur berbeda dalam urutan tertentu. pada permutasi
urutan diperhatikan, sehingga AB tidak samadenga BA.
Permutasi sendiri ada tiga macam.
- yang pertama adalah permutasi r unsur dari n unsur
- yang kedua adalah permutasi dengan beberapa unsur yang sama.
- dan yang terakhir adalah permutasi siklis.
adalah banyak permutasi r unsur dari n unsur, yang dinotasikan dengan P(n,r) detentukan oleh rumus:
adalah banyaknya permutasi dari n unsur yang memiliki r1 unsur pertama yang sama, r2 unsur kedua yang sama, . . . , dan rk unsur ke-k yang sama. Perhatika rumus dibawah ini!!!
Permutasi yang ketiga yaitu permutasi siklis.
adalah banyaknya permutasi siklis ( melingkar ) dari n unsur. Perhatikan rumus dibawah ini.
Rumus . (n-1)!
Setelah anda membaca tentang permutasi di atas apakah anda sudah memahaminya?
Jika sudah, coba kalian kerjakan soal dibawah ini, apakah menggunakan permutasi yang pertama,yang kedua, atau yang ketiga.
Perhatika soalnya baik-baik yah?
Soal Permutasi.
EBTANAS 1994.
Untuk menjabat pengelola suatu perusahaan memerlukan 3 staf pengurus yaitu ketua, sekretaris, dan bendahara. Tersedia 7 calon. banyaknya macam susunan staf pengurus yang mungkin adalah . . .
Apakah kalian bisa mengerjakan?, Pasti bisa donk yan?
mari kita cocokan pekerjaan kalian.
Pembahasan Permutasi.
Jika susunan staf pengurus adalah ABC, maka A sebagai ketua, B sebagai SEkretaris dan C sebagai bendahara. terapi jika susunan staf pengurus adalah , CBA maka C sebagai ketua, B sebagai Sekretaris dan A sebagai bendahara. Jadi jelas bahwa ABC tidak samadengan CBA. Ini berarti soal diatas memperhatikan urutan. Dengan demikian kita selesaikan dengan cara permutasi. pada soal diketahui bahwa akan dipilih 3 orang untuk menjadi staf Pengurusdari 7 orangcalon yang tersedia.
Hal ini merupakan permutasi 3 unsur dari 7 unsur. dengan demikian banyaknya susunan pengurus yang mungkin adalah .
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutan.
Rumus Kombinasi Adalah
Contoh soal Kombinasi.
1. ada lima orang dalam satu ruangan yang belum saling mengenal. apabilamereka ingin saling berkenalan dengan berjabat tangn sekali dengan setiap orang. maka banyaknya jabatan tangn yang terjafi adalah . . .
a. 5 kali
b. 10 kali
c. 15 kali
d. 20 kali
e. 25 kali
Semoga bermanfaat dan sukses buat kita semua dan lulus 100%. Amin.
trimakasih Wassalamualaikum Wr.Wb.
Sumber: http://sharematika.blogspot.no/
0 Soal dan Pembahasan Limit Fungsi Lengkap
Tutorial lumayan apik dan lengkap, silahkan download di bawa ini
0 Volume Benda Putar Metode Cincin
Pada Tutorial Maple kali ini, author akan membahas
mengenai bagaimana cara menghitung volume benda putar dengan metode
cincin menggunakan maple. Pada Tutorial Maple sebelumnya telah membahas bagaimana cara menghitung volume benda putar dengan metode cakram menggunakan maple.
Menghitung volume benda putar dengan menggunakan metode cincin dilakukan dengan memanfaatkan rumus volume cincin seperti gambar di bawah ini :
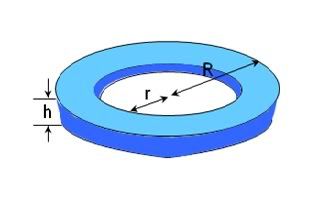
dari ilustrasi gambar di atas, kita dapat menentukan bahwa volume cincin di atas adalah
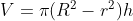
dimana R adalah jari-jari lingkaran besar
r adalah jari-jari lingkaran kecil
h adalah tebal cincin yang dapat dianggap sebagai tinggi cincin tersebut
Ada beberapa tahap yang harus diambil untuk menentukan volume benda putar dengan metode cincin
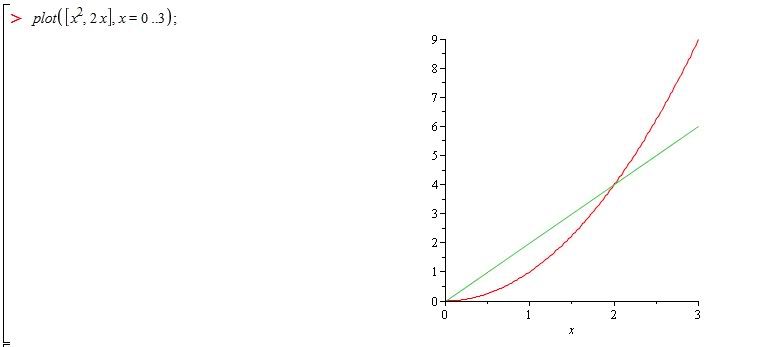
Dari gambar di atas kita tahu bahwa batas daerah yang kita cari adalah dari 0 sampai 2.
Untuk mendapatkan berapa volume daerah tersebut dengan menggunakan maple lakukan :
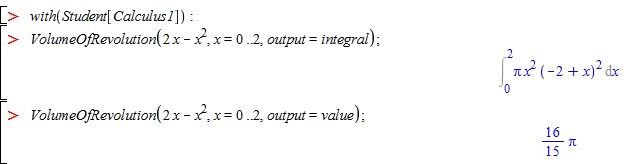
Hasil di atas menunjukkan bahwa volume benda putar yang dibatasi kurva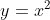
dan garis 
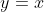diputar mengelilingi sumbu x sejauh 
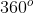adalah 
.
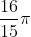Demikianlah Tutorial Maple pada kesempatan ini, semoga bermanfaat.
Selamat Mencoba
Sumber: http://sharematika.blogspot.no
Menghitung volume benda putar dengan menggunakan metode cincin dilakukan dengan memanfaatkan rumus volume cincin seperti gambar di bawah ini :
dari ilustrasi gambar di atas, kita dapat menentukan bahwa volume cincin di atas adalah
dimana R adalah jari-jari lingkaran besar
r adalah jari-jari lingkaran kecil
h adalah tebal cincin yang dapat dianggap sebagai tinggi cincin tersebut
Ada beberapa tahap yang harus diambil untuk menentukan volume benda putar dengan metode cincin
Dengan menggunakan maple kita dapat menentukan volume benda putar dengan mudah.
Langkah untuk menentukan volume benda putar dengan metode cincin dengan menggunakan maple yaitu :- Gambarlah daerahnya untuk mengetahui batasnya
- Panggil menu with(Student[Calculus1]);
- untuk menampilkan volume dalam bentuk integral tuliskan VolumeOfRevolution(fungsinya,intervalnya,diputar terhadap sumbu apa,output=integral)
- untuk menampilkan hasil volume tuliskan VolumeOfRevolution(fungsinya,intervalnya,diputar terhadap sumbu apa,output=value)
Untuk lebih jelasnya perhatikan contoh berikut !
Hitunglah volume benda putar yang terjadi jika daerah yang dibatasi kurva 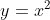dan garis 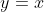diputar mengelilingi sumbu x sejauh !
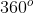- Pertama kita gambar terlebih dahulu untuk mengetahui daerahnya
Dari gambar di atas kita tahu bahwa batas daerah yang kita cari adalah dari 0 sampai 2.
Untuk mendapatkan berapa volume daerah tersebut dengan menggunakan maple lakukan :
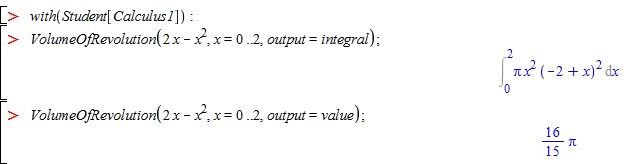
Hasil di atas menunjukkan bahwa volume benda putar yang dibatasi kurva
Demikianlah Tutorial Maple pada kesempatan ini, semoga bermanfaat.
Selamat Mencoba
Sumber: http://sharematika.blogspot.no
0 Penggunaan Turunan (Nilai Maksimum dan Minimum)
Pada tutorial maple sebelumnya telah dijelaskan penggunaan turunan untuk menguji kemonotonan dan kecekungan suatu fungsi, kali ini tutorial maple akan membahas mengenai penggunaan turunan untuk menentukan nilai maksimum dan minimum suatu fungsi.
Pengertian nilai Maksimum dan Minimum
Misalkan kita memiliki fungsi f(x) dan suatu domain S. Kita ingin menyelidiki apakah f(x) memiliki nilai maksimum atau minimum pada S atau tidak. Untuk kasus yang seperti ini kita membutuhkan konsep turunan untuk menyelesaikan masalah ini.
Untuk lebih jelasnya, akan dijelaskan definisi dari nilai maksimum dan minimum dari suatu fungsi, yaitu :
“ Jika f kontinu pada selang tertutup [a,b], maka f mencapai nilai maksimum dan minimum”
dari teorema tersebut jelaslah bahwa agar f memiliki nilai maksimum atau minimum maka f harus kontinu dan berada pada selang tertutup [a,b]
Untuk mencari nilai maksimum atau minimum dari suatu fungsi, kita membutuhkan titik – titik kritis. Lalu apa yang dimaksud dengan titik kritis? Berdasarkan Teorema Titik Kritis, yaitu
“andaikan f didefinisikan pada selang I yang memuat titik c. Jika f(c) adalah titik ekstrim, maka c haruslah suatu titik kritis, yakni berupa salah satu dari :
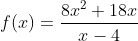
Pengertian nilai Maksimum dan Minimum
Misalkan kita memiliki fungsi f(x) dan suatu domain S. Kita ingin menyelidiki apakah f(x) memiliki nilai maksimum atau minimum pada S atau tidak. Untuk kasus yang seperti ini kita membutuhkan konsep turunan untuk menyelesaikan masalah ini.
Untuk lebih jelasnya, akan dijelaskan definisi dari nilai maksimum dan minimum dari suatu fungsi, yaitu :
- f(c) adalah nilai makasimum f pada S jika f(c) ≥ f(x) untuk semua x di S
- f(c) adalah nilai minimum f pada S jika f(c) ≤ f(x) untuk semua x di S
- f(c) adalah nilai ekstrim f pada S jka f(c) adalah nilai maksimum atau nilai minimum
“ Jika f kontinu pada selang tertutup [a,b], maka f mencapai nilai maksimum dan minimum”
dari teorema tersebut jelaslah bahwa agar f memiliki nilai maksimum atau minimum maka f harus kontinu dan berada pada selang tertutup [a,b]
Untuk mencari nilai maksimum atau minimum dari suatu fungsi, kita membutuhkan titik – titik kritis. Lalu apa yang dimaksud dengan titik kritis? Berdasarkan Teorema Titik Kritis, yaitu
“andaikan f didefinisikan pada selang I yang memuat titik c. Jika f(c) adalah titik ekstrim, maka c haruslah suatu titik kritis, yakni berupa salah satu dari :
- titik ujung dari I
- titik stasioner, yaitu titik c sehingga f’(c)=0
- titik singular, yaitu titik c dimana f’(c) tidak ada
dan nilai maksimum adalah nilai f(c)
terbesar ketika kita mensubstitusikan semua nilai kritis dalam fungsi f,
sedangkan nilai minimum adalah nilai f(c) terkecil ketika kita
mensubstitusikan semua nilai kritis dalam fungsi f.
Dalam maple, kita bisa menggunakan perintah “CriticalPoints” untuk mencari titik – titik kritis. Misal kita ingin mencari nilai Maksimum dan Minimum dari fungsi
Langkah – langkahnya :
- cari titik – titik kritisnya, yaitu dengan perintah “CriticalPoints”
- tuliskan with(Student[Calculus1]
- definisikan fungsi f(x)
f := (8*x^2+18*x)/(x-4)
- tuliskan CriticalPoints(f,x)
maka kita mendapatkan titik – titik kritis yaitu -1, 4, dan 9
- Selanjutnya kita substitusikan titik – titik tersebut pada f(x)
- Tuliskan subs(x=-1,f) dan kita mendapatkan nilai 2
- Tuliskan subs(x=4,f) dan fungsi menjadi tak terdefinisi
- Tuliskan subs(x=9,f) dan kita mendapatkan nilai 162
Yang merupakan nilai maksimum adalah 162 dan nilai minimum adalah 2
Selamat Belajar
Sumber: http://sharematika.blogspot.no
1 Mencari Volume Benda Putar dengan Metode Cakram
Pada tutorial maple sebelumnya kami telah membahas bagaimana cara untuk menentukan luas suatu daerah dibawah kurva f(x) yaitu dengan Integral.
Lalu bagaimana dengan volumenya?
Apabila sebuah daerah rata, yang teretak seluruhnya pada satu bagian bidang yang terbagi oleh sebuah garis lurus tetap diputar mengelilingi garis tetap tersebut, maka daerah itu akan membentuk suatu benda putar.
Bagaimana cara untuk menentukan volume benda putar tersebut?
Dalam kalkulus ada 3 cara untuk menentukan volume benda putar, yaitu dengan metode cakram,metode silinder (kulit tabung), dan metode cincin. Tutorial maple kali ini akan membahas bagaimana menentukan volume suatu benda putar dengan Metode cakram. Sebelum lanjut pada penggunaan dengan maple, akan dibahas terlebih dahulu gambaran mengenai metode cakram .
Disebut metode cakram karena apabila suatu benda putar dipartisi menjadi beberapa bagian maka partisi tersebut membentuk suatu cakram.
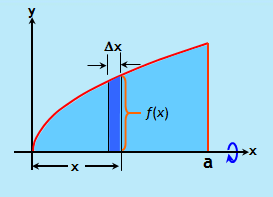
bentuk cakram diatas dapat dianggap sebagai tabung dengan jari – jari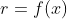
, tinggi 
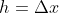. sehingga volumenya dapat diaproksimasi sebagai 
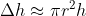atau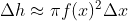 
.
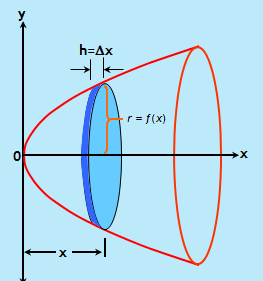
partisi tersebut merupakan bagian dari keseluruhan volume benda putar, sehingga volume benda putarnya dapat dinyatakan sebagai
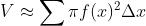
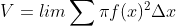
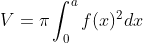
Contoh :
Tentukan volume benda putar yang dibatasi oleh kurva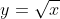
, sumbu 
, dan garis x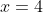
apabila diputar mengelilingi sumbu .
Penyelesaian :
Pertama, gambarkan dulu benda putarnya dan buat partisi-partisinya.
Dari gambar kita dapatkan partisi dari benda putar tersebut berupa cakram yang memiliki volume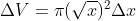
dan volume benda putarnya adalah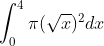
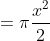for from 0 to 4.
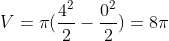
dengan menggunakan maple, langkah – langkahnya adalah sebagai berikut:
1. tuliskan with(Student[Calculus1])
2. pilih perintah VolumeOfRevolution
3.. tuliskan VolumeOfRevolution(sqrt(x), x = 0 .. 4, axis = horizontal, output = integral) untuk melihat bentuk integralnya,
4.. tuliskan VolumeOfRevolution(sqrt(x), x = 0 .. 4, axis = horizontal, output = animation) untuk melihat gambarnya, dan
5. tuliskan VolumeOfRevolution(sqrt(x), x = 0 .. 4, axis = horizontal, output = value) untuk mengetahui hasilnya
Perhatikan bahwa pada penulisan axis=horizontal menunjukkan bahwa pemutaran benda putar ini adalah terhadap sumbu, jika benda putar diputar terhadap sumbu 
maka penulisannya adalah axis=vertical
animasi atau gambar tersebut bisa diputar-putar lo… unik kaan?
bagaimana? mudah bukaaan?
semoga bermanfaat
Sumber: http://sharematika.blogspot.no
Lalu bagaimana dengan volumenya?
Apabila sebuah daerah rata, yang teretak seluruhnya pada satu bagian bidang yang terbagi oleh sebuah garis lurus tetap diputar mengelilingi garis tetap tersebut, maka daerah itu akan membentuk suatu benda putar.
Bagaimana cara untuk menentukan volume benda putar tersebut?
Dalam kalkulus ada 3 cara untuk menentukan volume benda putar, yaitu dengan metode cakram,metode silinder (kulit tabung), dan metode cincin. Tutorial maple kali ini akan membahas bagaimana menentukan volume suatu benda putar dengan Metode cakram. Sebelum lanjut pada penggunaan dengan maple, akan dibahas terlebih dahulu gambaran mengenai metode cakram .
Disebut metode cakram karena apabila suatu benda putar dipartisi menjadi beberapa bagian maka partisi tersebut membentuk suatu cakram.
bentuk cakram diatas dapat dianggap sebagai tabung dengan jari – jari
partisi tersebut merupakan bagian dari keseluruhan volume benda putar, sehingga volume benda putarnya dapat dinyatakan sebagai
Contoh :
Tentukan volume benda putar yang dibatasi oleh kurva
Penyelesaian :
Pertama, gambarkan dulu benda putarnya dan buat partisi-partisinya.
Dari gambar kita dapatkan partisi dari benda putar tersebut berupa cakram yang memiliki volume
dan volume benda putarnya adalah
dengan menggunakan maple, langkah – langkahnya adalah sebagai berikut:
1. tuliskan with(Student[Calculus1])
2. pilih perintah VolumeOfRevolution
3.. tuliskan VolumeOfRevolution(sqrt(x), x = 0 .. 4, axis = horizontal, output = integral) untuk melihat bentuk integralnya,
4.. tuliskan VolumeOfRevolution(sqrt(x), x = 0 .. 4, axis = horizontal, output = animation) untuk melihat gambarnya, dan
5. tuliskan VolumeOfRevolution(sqrt(x), x = 0 .. 4, axis = horizontal, output = value) untuk mengetahui hasilnya
Perhatikan bahwa pada penulisan axis=horizontal menunjukkan bahwa pemutaran benda putar ini adalah terhadap sumbu
animasi atau gambar tersebut bisa diputar-putar lo… unik kaan?
bagaimana? mudah bukaaan?
semoga bermanfaat
Sumber: http://sharematika.blogspot.no
Langganan:
Postingan (Atom)
